The sigmoid function is a continuous, monotonically increasing function with a characteristic 'S'-like curve, and possesses several interesting properties that make it an obvious choice as an activation function for nodes in artificial neural networks.
The domain of the sigmoid function is the set of all real numbers, \(\mathbb{R}\),
and it's defined as:
Please note that equation \eqref{eq:sigmoid_function} could just as well
be written as \(\sigma(x) = \frac{e^x}{{e^x} + 1}\) (this is seen by multiplying
equation (1) by \(\frac{e^x}{e^x}\), i.e. multiplying by 1).
$$\begin{equation}
\label{eq:sigmoid_function}
\sigma(x) = \frac{1}{1 + e^{-x}}
\end{equation}$$
The graph of the sigmoid function illustrates its smooth, gradual transition from values just above \(0\) to values just below \(1\) - a transition that almost fully occurs in the interval \(-5 \lt x \lt 5\).
For arguments near \(0\) the sigmoid function approximates a linear function with slope \(\frac{1}{4}\).
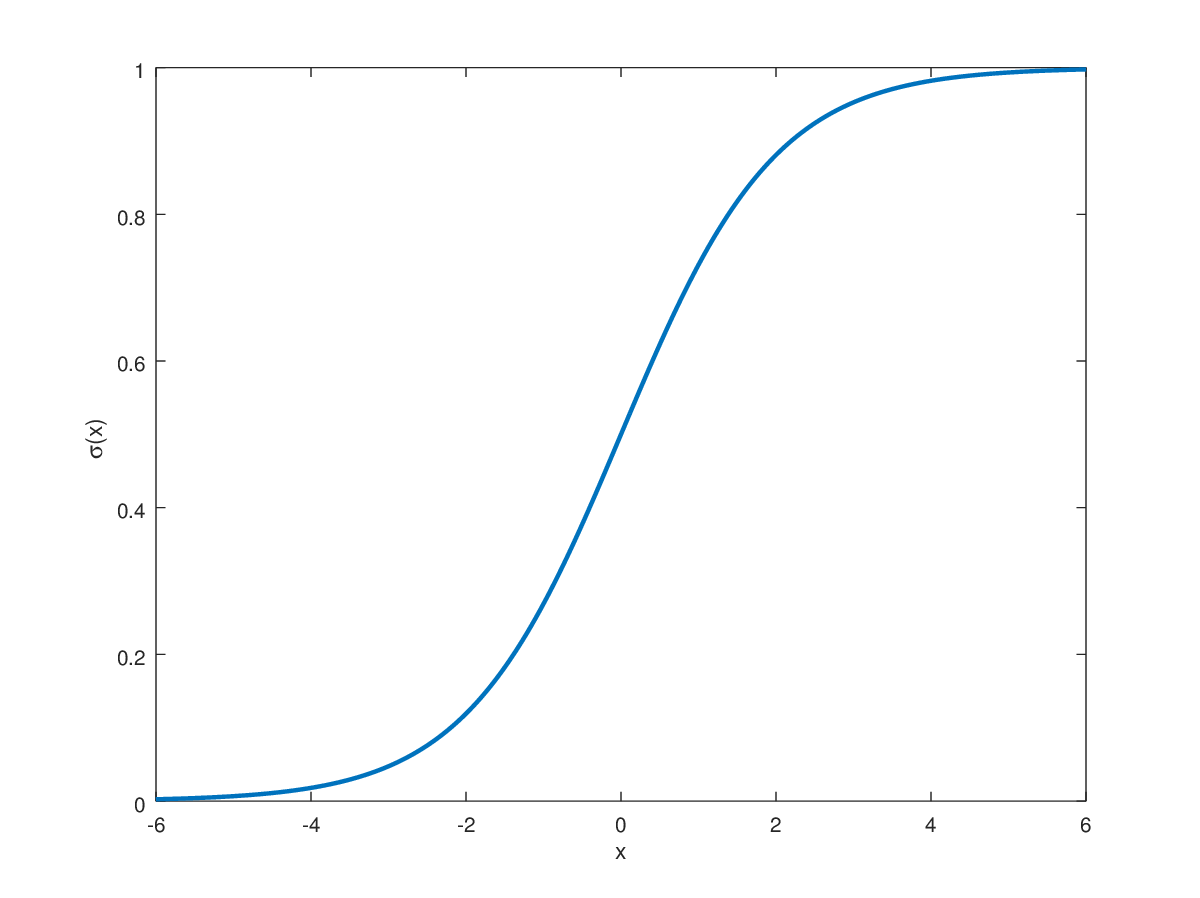Figure 1: The elongated 'S'-like curve of the sigmoid function
From equation \eqref{eq:sigmoid_function} (and the smooth curves of the figure above) it's clear *As \(x\) gets larger the value of \(e^{-x}\) tends towards \(0\), and as as \(x\) approaches negative infinity the value of \(e^{-x}\) grows to be infinitely large. that as \(x\) gets larger the value of \(\sigma(x)\) tends towards \(1\)*. Similarly it should be evident that the limit of \(\sigma(x)\), as \(x\) approaches negative infinity, is \(0\). That is:
$$\begin{equation} \lim\limits_{x \to \infty} \sigma(x) = 1 \end{equation}$$ $$\begin{equation} \lim\limits_{x \to -\infty} \sigma(x) = 0 \end{equation}$$I.e. the range of \(\sigma(x)\) are real numbers in the interval \(]0, 1[\), and there's a "soft step" between the off and on values represented by the extremes of its range. As mentioned above the sigmoid function is a function with domain over all \(\mathbb{R}\), so we can sum this up as:
$$\begin{equation} \sigma : \mathbb{R} \to ]0, 1[ \end{equation}$$Also note that \(\sigma(x)\) has rotational symmetry with respect to the point \((0, \frac{1}{2})\), and the sum of the sigmoid function and its reflection about the vertical axis, \(\sigma(-x)\) is
$$\begin{equation} \label{eq:sigmoid_function_symmetry} \sigma(x) + \sigma(-x) = 1 \end{equation}$$We'll rely on this property when finding the derivative of the sigmoid function, so let's prove it in detail.
$$\begin{align} \sigma(x) + \sigma(-x) &= \frac{1}{1 + e^{-x}} + \frac{1}{1 + e^{-(-x)}} \notag \\ &= (\frac{1 + e^{x}}{1 + e^{x}}) \cdot \frac{1}{1 + e^{-x}} + (\frac{1 + e^{-x}}{1 + e^{-x}}) \cdot\frac{1}{1 + e^{x}} \notag \\ &= \frac{(1 + e^{x}) + (1 + e^{-x})}{(1 + e^{-x}) \cdot (1 + e^{x})} \notag \\ &= \frac{2 + e^{x} + e^{-x}}{1 + e^{x} + e^{-x} + e^{-x+x}} = \frac{2 + e^{x} + e^{-x}}{2 + e^{x} + e^{-x}} \notag \\ &= 1 \notag \end{align}$$The derivative of the sigmoid function
Another interesting feature of the sigmoid function is that it's differentiable (a required trait when back-propagating errors).
The derivative itself has a very convenient and beautiful form:
$$\begin{equation} \label{eq:sigmoid_function_derivative} \frac{d\sigma(x)}{dx} = \sigma(x) \cdot (1 - \sigma(x)) \end{equation}$$This means that it's very easy to compute the derivative of the sigmoid function if you've already calculated the sigmoid function itself. E.g. when backpropagating errors in a neural network through a layer of nodes with a sigmoid activation function, \(\sigma(x)\) has already been computed during the forward pass.
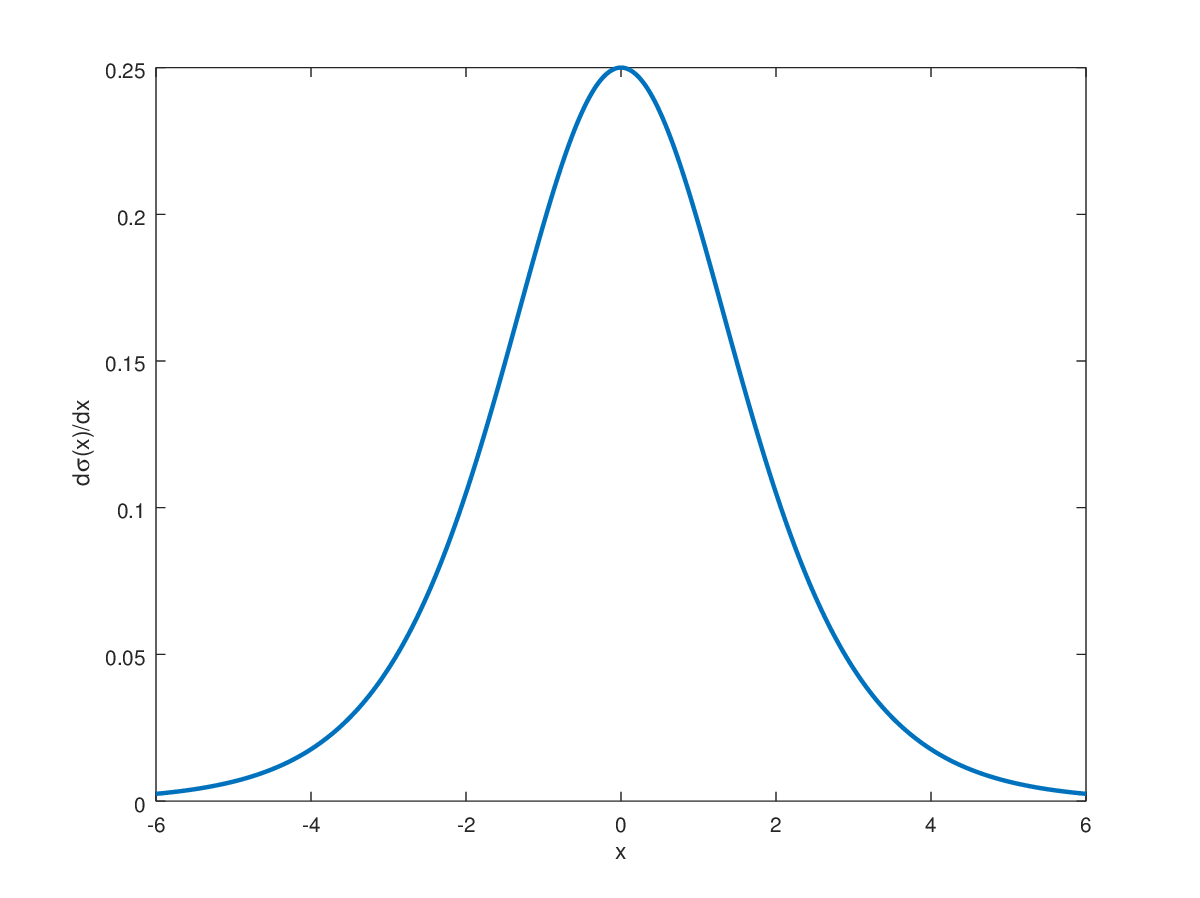Figure 2: The bell-shaped curve of the derivative of the sigmoid function
In order to differentiate the sigmoid function as shown in equation \eqref{eq:sigmoid_function_derivative} we'll first derive:
$$\begin{equation} \label{eq:sigmoid_function_derivative_sigma_x_times_sigma_minus_x} \frac{d\sigma(x)}{dx} = \sigma(x) \cdot \sigma(-x) \end{equation}$$Then equation \eqref{eq:sigmoid_function_derivative} follows directly from the above fact combined with equation \eqref{eq:sigmoid_function_symmetry} (which tells us that \(\sigma(-x) = 1 - \sigma(x)\)). So here goes:
To differentiate the sigmoid function we rely on the composite function rule (a.k.a the chain rule) and the fact that \(\frac{d(e^{x})}{dx}=e^{x}\). The composite function rule says that if \(f(x) = h(g(x))\) then the derivative of \(f\) is \(f'(x) = h'(g(x)) \cdot g'(x)\), or put in plain word: you first differentiate the ‘outside’ function, and then multiply by the derivative of the ‘inside’ function. $$\begin{align} \frac{d\sigma(x)}{dx} &= \frac{d}{dx}(\frac{1}{1 + e^{-x}}) \notag \\ &= \frac{d}{dx}(1 + e^{-x})^{-1} \notag \\ &= -(1 + e^{-x})^{-2} \cdot (-e^{-x}) \notag \\ &= \frac{e^{-x}}{(1 + e^{-x})^{2}} \notag \\ &= \frac{1}{1 + e^{-x}} \cdot \frac{e^{-x}}{1 + e^{-x}} \notag \\ &= \sigma(x) \cdot \sigma(-x) \notag \\ \end{align}$$
Where the last equality follows directly from equation \eqref{eq:sigmoid_function} (please refer to the margin note for \eqref{eq:sigmoid_function}, for the alternate form of the sigmoid function).
As should be evident from the graph of the derivative of the sigmoid function it's symmetric across the vertical axis, that is:
$$\begin{equation} \label{eq:sigmoid_function_derivative_symmetri} \frac{d\sigma(x)}{dx} = \frac{d\sigma(-x)}{dx} \end{equation}$$This can also easily be seen from equation \eqref{eq:sigmoid_function_derivative_sigma_x_times_sigma_minus_x}, as shown by the following: \(\frac{d\sigma(x)}{dx} = \sigma(x) \cdot \sigma(-x) = \sigma(-x) \cdot \sigma(-(-x)) = \frac{d\sigma(-x)}{dx}\)