The unit step function models the on/off behavior of a switch. It is also known as the Heaviside function named after Oliver Heaviside, an English electrical engineer, mathematician, and physicist.
The unit step function is a discontinuous function that can be used to model e.g. when voltage is switched on or off in an electrical circuit, or when a neuron becomes active (fires).
The domain of the unit step function is the set of all real numbers, \(\mathbb{R}\),
and it's defined as:
Sometimes the unit step function is defined as \(u(x) = \begin{cases}
0 \text{, if } x \lt 0 \\
\frac{1}{2} \text{, if } x = 0 \\
1 \text{, if } x \gt 0
\end{cases}\)
in which case the graph has rotational symmetry. But for our need the pure on/off behaviour suffices.
$$\begin{equation}
\label{eq:unit_step_function}
u(x) = \begin{cases}
0 \text{, if } x \lt 0 \\
1 \text{, if } x \ge 0
\end{cases}
\end{equation}$$
Moving along the \(x\)-axis from negative infinity to positive infinity, the unit step function assumes
a constant value of \(0\) until the threshold input, \(x=0\), is reached, after which the function
assumes a constant value of \(1\). This is illustrated in figure 1.
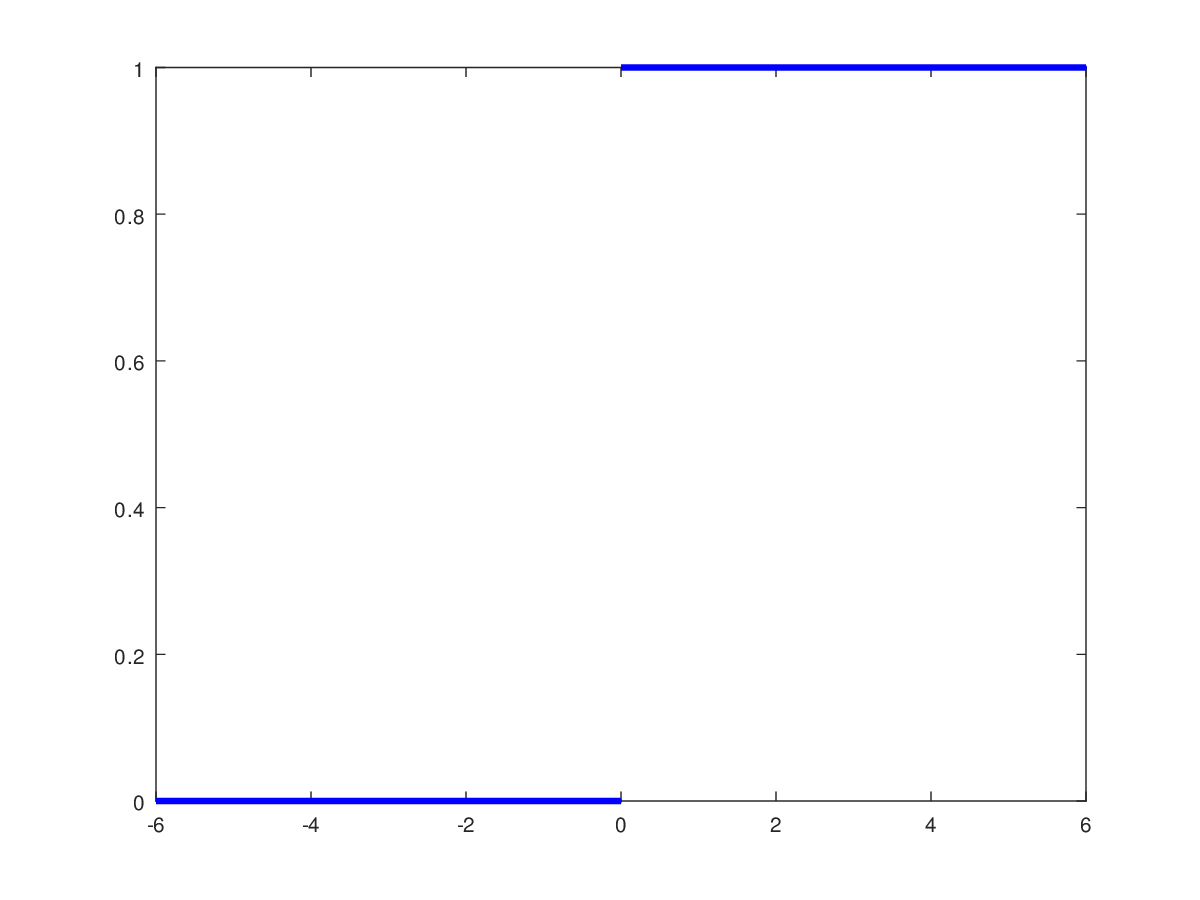Figure 1: The unit step function
Shifted unit step function
If you instead want the unit step function to "switch" at a different threshold value, \(t\), then the function can be shifted (or delayed) to this other threshold. The easiest way to see this is to insert the shifted value \(x' = x - t\) in equation \eqref{eq:unit_step_function}, which gives us $$\begin{equation} \label{eq:shifted_unit_step_function} u_t(x) = u(x - t) = \begin{cases} 0 \text{, if } x \lt t \\ 1 \text{, if } x \ge t \end{cases} \end{equation}$$ Figure 2 illustrates a unit step function shifted to a non-zero threshold value, \(t = 42\).
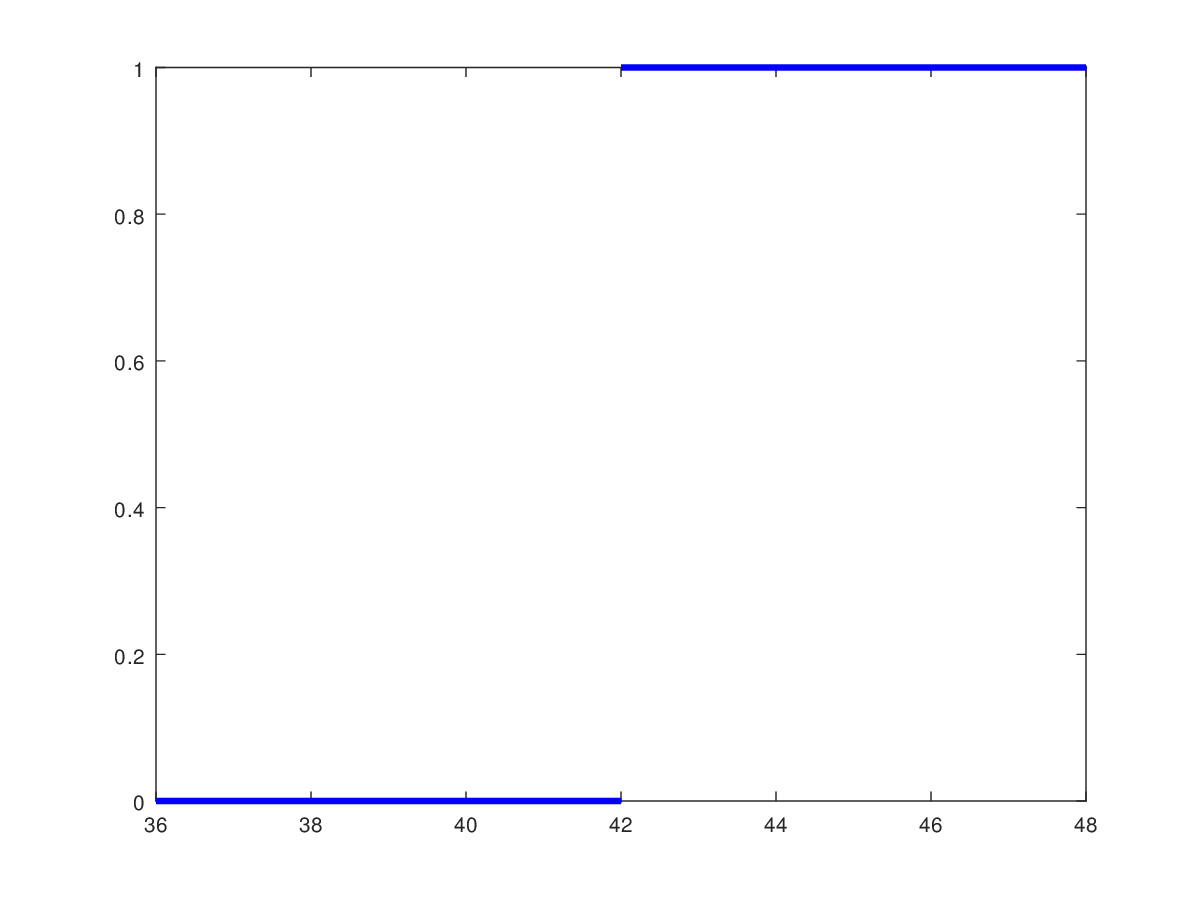Figure 2: The unit step function with a non-zero threshold
The derivative of the unit step function
As the unit step function is discontinuous at its threshold value, the function is not differentiable.
This is also relatively easy to see from equation \eqref{eq:unit_step_function}, where approaching \(x = 0\) from the left (the negative side) of the \(x\)-axis gives us $$\begin{equation} \lim\limits_{h \to 0^-} \frac{u(0+h)-u(0)}{h} = \lim\limits_{h \to 0^-} \frac{0-1}{h} = \infty \end{equation}$$ meaning that the unit step function is not differentiable at the point of its discontinuity.
That being said, the derivative of the unit step function \eqref{eq:unit_step_function} at all other points than its threshold, \(x=0\), is also pretty boring, as it assumes the constant value of \(0\). That is $$\begin{equation} \label{eq:unit_step_function_derivative} \frac{du(x)}{dx} = 0 \text{, for } x \ne 0 \end{equation}$$ This also means that the unit step function is useless in connection with backpropagation that relies on the derivative of its activation function for weight adjustments, i.e. there would be no change for any value other than zero (where the change would be infinite).
Still, the unit step function is included here as it plays an important role in the description of perceptrons.